Il y a 3700 ans, les savants de Babylone utilisaient déjà des tables trigonométriques ! Voilà ce que viennent de découvrir des chercheurs australiens qui ont réussit à traduire une tablette cunéiforme : la Plimton 322.

Mais commençons d’abord par nous rafraîchir la mémoire et une petit rappel sur Babylone et la trigonométrie.

Babylone capitale de la Mésopotamie

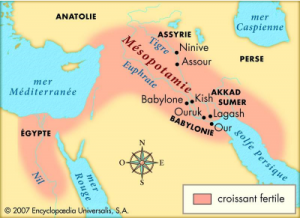Babylone fut la capitale d’un vaste empire qui a régné durant l’Antiquité sur la Mésopotamie, (c’est-à-dire l’Irak et la Syrie actuelle).

La civilisation mésopotamienne, qui a duré trois millénaires, fut aussi brillante que sa sœur jumelle : l’Égypte pharaonique. Les Mésopotamiens ont même précédé l’Egypte dans toute une série d’inventions fondamentales. Les premiers ils ont inventé l’écriture, les mathématiques, l’astronomie, la roue, la charrue, l’irrigation, l’architecture, la ville, l’État, le droit, l’école, la médecine, la mythologie ! Oui tout cela est apparu pour la première fois en Mésopotamie.

Cette civilisation est moins célèbre que celle de l’Egypte parce qu’elle n’a pas laissé des vestiges de pyramides ou des temples en ruine. Ce n’est pas faute d’en posséder : la « tour de Babel » de la Bible n’est rien d’autre que l’immense tour construite à Babylone ; Le roi Nabuchodonosor 1^er fit construire des jardins suspendus sur les terrasses de son palais. Et les historiens de l’Antiquité en parlaient comme l’une des sept merveilles du monde.

Mais ces bâtiments furent construits en briques d’argile et non en pierres. Ils n’ont pas résisté au temps. Quand l’empire babylonien s’effondra, les tours et les monuments se sont désagrégés. A l’époque de Jésus christ (600 ans après sa conquête et son pillage par les armées perses), Babylone, situé à 150 Km au sud de Bagdad, n’était déjà plus qu’un vestige en train de disparaître sous les sables (comme les autres grandes villes qui avait fait la gloire de la Mésopotamie. Il faut attendre au 19^ème siècle pour que des explorateurs et archéologues soient avertis par des paysans de l’existence montagnes de ces briques ensevelis sous le sable. Peu à peu mis à jour le trésor qu’elles recelait.

Car si les monuments furent engloutis, en revanche, les tablettes d’argile sur lesquels les mésopotamiens écrivaient ont mieux résisté au temps que les papyrus Égyptiens. Ces tablettes écrites en cunéiforme ont traversé les siècles sous les sables chaud du désert. Depuis le 19^ème siècles des centaines de milliers de tablettes (500 000 environ !) ont été mis a jour par les archéologues.

Et il a fallu la patience et l’érudition de centaines d’assyriologues pour réussir à déchiffrer cette écriture. Mais elle a conduit a dévoiler peu à peu la richesse de cette civilisation légendaire. Sur les tablettes cunéiformes ont trouve de tout[1]  : des récits mythologique (comme la légendaire de Gilgamesh et le mythe du déluge), des textes de lois, des traités de médicaux, des lettres diplomatiques, des comptes publics, des données astronomiques, des manuels scolaires avant l’heure. Et aussi nombreux écrits mathématiques: dont cette fameuse tablette : «  Plimpton 322 ».

Pour la petite histoire, cette tablette a été trouvé dans les années 1920 par Edgar J. Banks , un archéologue-antiquaire, chasseur de trésor et pilleurs de tombe comme il en existait à l’époque (on dit qu’il aurait servi de modèle pour le personnage d’Indiana Jones). Edgar J. Banks a vendu la tablette à un riche éditeur-yorkais Georges A. Plimpton (à une époque où vendre des livres rapportait de l’argent) qui l’a cédé à sa mort à l’université de Columbia.

Cette tablette a été étudié par des générations de chercheurs [2] et a donné lieu jusque là à multiples spéculations. Jusqu’à ce que deux chercheurs australiens, Daniel Mansfield et Norman Wildberger réussissent enfin à en décrypter le sens précis.

A quoi sert la trigonométrie ?

Deuxième petit rappel : qu’est-ce que la trigonométrie ? Pour beaucoup c’est un instrument de torture pour collégiens où il est question de sinus, cosinus et tangente.

A part ça, la trigonométrie, c’est la science du « trigone », l’autre nom du triangle (en latin angle se dit angulus, en grec il se dit « gone » : le trigone est donc le plus simple des « polygone ». Et il a une vertu mathématique: toutes les figures géométriques, si biscornues soit-elles, peuvent se ramener à une somme de triangles. Etudier les triangles, les relations entre les angles et les côtés, c’est donc pouvoir mesurer le monde.

Voilà a quoi sert la trigonométrie.

Dans l’antiquité ce fut une découverte fondamentale pour les arpenteurs, les architectes, les astronomes, les marins et cartographes. La mesure des triangles permet ce tour de force: calculer la distance entre l’endroit où vous vous êtes actuellement et un autre point lointain mais inaccessible (le sommet d’une montagne, la distance à l’île que le bateau voit à l’horizon). Il suffit de deux angles de vue différents pour calculer cette distance inconnue. La méthode la « triangulation ».

La triangulation a permis de tracer des routes ou des réseaux d’irrigation, de tracer des cartes, édifier des tours et des palais.

Voilà a quoi sert une table de trigonométrie : donnez moi un angle et une longueur et je vous donnerait je vous calcule la distance de la lune.

Voilà ce que l’on trouve sur la tablette Plimpton 322 : les bases élémentaires de la trigonométrie ! Et elle date de 1700 ans avant J.-C. On croyait jusque là que les tables de trigonométrie était une invention bien plus tardive et qui remontait aux grecs.

Un calcul plus simple que le nôtre !

La tablette Plimpton 322

Mais il y a mieux : le mode de calcul des babyloniens était plus simple que celui utilisé des siècles plus tard par les savants grecs, arabes ou occidentaux !

En effet, les babyloniens calculait en base 60, comme on le fait aujourd’hui pour diviser les heures et les minutes. C’est d’ailleurs eux qui nous ont légué ce mode de calcul du temps.

Quand on apprend à compter les heures, ce système en base 60 paraît plus compliqué que le système décimal. Pourtant il est parfois plus commode. Dans le système décimal, quand on divise une mètre par 2 ( cela on obtient 5 centimètres) mais divisé 3, c’est déjà plus compliqué, : ça donne 3, 3333 cm qui n’est pas un chiffre rond.

En revanche, quand vous divisez une heure en deux, ça donne 30 minutes (ou une demi -heure), divisez trois, cela fait 20 minutes (encore une chiffre rond), divisez par quatre, cela fait quinze minutes (notre quart d’heure : toujours une chiffre rond…), c’est encore le cas pour la division par par cinq, par six : toujours des chiffres ronds que l’on peut exprimer en fractions :1/2, 1/3, 1/4, 1/5, etc.

La trigonométrie des babyloniens, fondée sur une système à base 60, permettait donc de noter les valeurs des triangles et des côtés par des fractions de nombre entiers, (1/2 ou 1/3 ou 1/4, etc.) ce qui était beaucoup plus facile qu’avec nos valeur de sinus, cosinus, qui sont toujours des nombres compliqués (du genre, 2,64, 5, 61 ou ou 3,34 ). A bien des égards, la trigonométrie à Babylone était non seulement bien antérieure de plus d’un millénaire à celle des grecs mais elle était plus simple !

Sources : « Plimpton 322 is Babylonian exact sexagesimal trigonometry », Daniel Mansfield et Norman H. Wildberger, Historia Mahématica, août 2017. En ligne :

Si maintenant si vous vous demandez, pourquoi les mésopotamiens ont au inventé aussi l’écriture, l’astronomie, la roue, la charrue, l’architecture, la ville et l’État ?  précipitez vous sur l’article j’ai publié dans Eureka, Histoire des grandes découvertes : Tout commence en Mésopotamie.